真实传达信号　DAC起到数字/模拟转换的作用

真实世界并非全然是数字环境，电子信号亦非由逻辑高低值或零与一组成，这些信号都是在某个电压或电流范围内的模拟信号，而数字模拟转换器(DAC)的用途就是将数字数据转换为模拟信号。数字数据可能来自于微处理器、高效能特定应用集成电路(ASIC)或现场可编程门阵列(FPGA)，但是须要转换成模拟信号，才能对真实世界产生影响。无论系统使用的是音讯放大器、发光二极管(LED)指示器还是马达驱动器，最终信号的本质都会是模拟信号。数字模拟转换器正是将数字信号传输至模拟世界的桥梁，最终目的就是希望能准确而真实地传达信号。数字模拟转换器是许多电子系统中的重要零件，所以了解其相关基础知识大有帮助。本文将介绍数字模拟转换器基本操作、关键定义及常见的拓扑。

DAC重新建构采样数据 

自Nyquist-shannon采样定理出现以来，工程师们就在开发及使用数字模拟转换器，但仅在过去的25年中，单芯片数字模拟转换器才受到广泛应用。根据Nyquest-shannon采样定理，只要符合频宽与Nyquest标准，任何采样数据都可完美地重新建构。因此透过适当设计，数字模拟转换器就能在应用中准确地重新建构采样数据。 

图1所示为4位并联输入数字模拟转换器的示意图。4位数字模拟转换器有24，也就是十六种可能的输入数据代码，如表中的第一栏所示。对于输入数据代码，数字模拟转换器可使用普通二进制或二补码系统，其中普通二进制最为常见。数字模拟转换器具模拟参考(VREF)及电源供应器(VA)与模拟输出。在许多情况下，模拟参考及电源电压可以相同，因此数字模拟转换器的一个接脚可用于两种功能，同时参考可视数字模拟转换器设计所需决定是电压或电流。数字模拟转换器用参考乘以输入数据代码来产生模拟输出，因此数字模拟转换器是模拟数字转换器(ADC)的反函数。模拟数字转换器是一种除法，将模拟输入转换为数字位。数字模拟转换器可视设计所需决定电压或电流输出。电流输出数字模拟转换器特别适合高频应用，在这些应用中可能需要更高的准确度，这可透过内建电流至电压转换来实行。此外，某些类型的数字模拟转换器使用双极(正极及负极)，而不是单极结构，这种结构可用于建立二象限与四象限乘法数字模拟转换器。本文将重点介绍单极电压输出数字模拟转换器，读者可由此轻松掌握其它数字模拟转换器结构的理论。 

图1数字至模拟转换器操作

图1最低有效位(LSB)是数据代码最右侧的位，表示数字代码中的最小值；最高有效位(MSB)是数据代码最左侧的位，也表示一半的量测值。如表中所示，LSB(0001b)表示0.3125伏特(V)，LSB值由以下方程序决定(方程式1)： 

(方程式1)  

在大多数数字模拟转换器中，增益(G)为1，这样可将方程式简化为VREF/2N。在理想的数字模拟转换器设计中，每增加一个位，就会使输出电压增加一个LSB。在本范例中，一个LSB的值是0.3125伏特，这是数字模拟转换器可解析的最小增量。将LSB值与数据输入代码(DIN)相乘，即可将基本传输函数以以下的方程式2表示： 

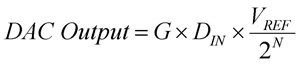
(方程式2)  

当DIN为1111时，数字模拟转换器的输出如方程式3所示。由此可知本范例中的最大输出值为低于电压参考(5伏特)一个LSB(0.3125伏特)的值。 

(方程式3)

在以上的范例中，输出电压只能上升到低于满标(Full-scale)电压一个LSB的值。这在许多数字模拟转换器中很常见，但某些数字模拟转换器经过特殊设计，允许最大输出电压达到满标电压。 

数字模拟转换器正确传达模拟信号的关键因素为数字模拟转换器的分辨率，或其可产生的信号「准确度」。从方程式1中可看出，LSB值与位数(N)成反比，与VREF成正比，所以位数增加将会使LSB值减小，结果会导致数字模拟转换器分辨率提高且信号准确度更佳。图2所示为「真实世界」正弦波形及4位与6位数字模拟转换器的实例。数字模拟转换器输出应透过数学方式以离散点方式表示，但由于存在延迟时间，操作中的数字模拟转换器输出方式将类似于众所周知的「梯度」信号(如同示波器上所示)。要注意的是降低参考电压同样也可提高分辨率，但这将导致较低的满标输出范围，因为可获得的最大输出值会受到VREF-1 LSB的限制。 

图2正弦曲线和DAC分辨率

数字模拟转换器基本操作很容易理解，但半导体制造商之间使用的术语可能有些混乱甚至相互矛盾。因此对设计师来说，了解应用中大多数数字模拟转换器数据表上所示的关键参数含义(表1)至关重要。 

DAC拓扑变化多 

字符串DAC是最常用的数字模拟转换器之一，并且有许多可用的变化。其中包括基本开尔文(Kelvia)除法器、二进制加权式DAC、以数位电位计为主的DAC、分段式字符串DAC及其它类型。开尔文除法器也称为字符串除法器，是最简单、也很常见的数字模拟转换器拓扑。 

在图3的拓扑中，对每个节点上具有开关的内部电阻器与逻辑区块对二进制输入进行译码，N位数字模拟转换器将包含2N个电阻器及2N个开关。此拓扑具电压输出，使用完全相符的电阻器时，具有线性单调性，主要缺点是输出阻抗较高。大多数供货商都会增加内部放大器作为输出缓冲器，为后续电路提供低阻抗来源，通常会视数字模拟转换器的分辨率来决定是否须要使用大量电阻器/开关。4位数字模拟转换器仅需要十六个电阻器/开关，而中等分辨率的12位DAC将需要四千零九十六个。随着科技的进步，这种拓扑在高达12?14位的数字模拟转换器中也很常见。在字符串除法器图的右侧可看到DAC121S101整合放大器缓冲器，并使用串行周边总线(SPI)接口来输入数据与进行控制。 

图3尔文除法器和12位字符串除法器-DAC121S101

R-2R梯形DAC是另一种很常见的拓扑。图4中的电压输出DAC使用电阻器的两个值比率为2比1。如图4所示，电阻器的数量相较于字符串数字模拟转换器大大减少。任何R2-R DAC都只需要2N个电阻器，这样就更容易调整电阻器值。因此4位数字模拟转换器只需要八个电阻器，8位数字模拟转换器只需要二十四个电阻器。在图4的右侧是DAC0831，其中包含并联输入代码缓存器，以及用于微处理器连接的支持功能区块。 

图4 R-2R梯形

R-2R梯形可设计成具有电压或电流输出。使用电压输出的主要好处是输出阻抗不变，更容易连接输出端的缓冲放大器。随着科技的改进，目前已开发出多种R-2R梯形拓扑的变化，这点与字符串数字模拟转换器非常相似。 

乘法型DAC(MDAC)就是基于R-2R梯形的变化。由于可透过互补式金属氧化物半导体(CMOS)开关控制R-2R开关，因此很容易建构梯形，以便在输入端使用双极信号。在输入端使用正负双极信号，就可将拓扑设计成启用二象限与四象限数据存取组件(MDACs)。这些MDACs通常用作可变增益放大器，但除此用途之外，还有许多独特的应用。 

分段式DAC是一种可混合或串联多种其它数字模拟转换器架构(字符串或R-2R梯形)的拓扑。这些专业化DAC常用于高速视讯或音讯系统中，在这些系统中重新建构信号须跨越大范围电压或频率来执行。 

Sigma Delta(Σ-Δ)DAC是「相对」较新的拓扑，其操作与增量总和模拟数字转换器相似。这种数字模拟转换器电路以低速率接收输入数据，并以高速率将零新增到数据串流中，然后以高速率随着时间推移进行过滤。接着会透过将数据转换成位串流的Σ-Δ调变器来传递数据串流，最后再透过总和小于参考电压之间切换的1位数字模拟转换器来传递数据串流。 

Sigma Delta DAC(及ADC)因其高分辨率与良好的DNL而广受欢迎。Sigma Delta DAC应用包括校准、音讯及声带系统，在频宽方面受到限制，因此不用于高速应用。 

电子设计中，数字模拟转换器在数字数据转换为模拟信号时发挥重要作用。数字模拟转换器可用于校准系统、马达控制、工厂测试设备、音讯系统、测量设备、控制系统与许多其它装置中。但与数字模拟转换器同样重要的是，设计工程师应切记它只是系统的一部分，而系统可包含处理器、内存、电源供应器、模拟电路及其它混合信号装置，这些功能区块透过架构联系在一起，影响数字模拟转换器电路的因素，例如噪声与误差，也会影响架构的其它区块。